On data representation in GHC Haskell

November 13, 2015 - Tagged as: en, haskell.

It’s been a while since last time I wrote a blog post. This is not because I don’t have anything to write, rather, I have too much to write, and I was afraid that if I start writing it’d take too long.

But now that I started writing stuff for different applications(fellowships, internships etc.) I thought maybe this is a good time to write some blog posts too.

At ICFP this year¹ we initiated a discussion about data representation in GHC Haskell. My advisor gave lightning talk at HIW(Haskell Implementors Workshop). It’s a 5-minute talk and I recommend everyone reading this blog post to watch it. In the presentation, he showed this plot: (click on it to maximize)

I put that here as a reference, but I’ll actually use some more detailed plots and correct a mistake in that plot. You can generate all the plots I show here using my benchmark programs here.

In this post I want to make a point that is similar to Ryan’s point in the lightning talk: In Haskell, we’re not doing good job in data layouts. Our data is lazy by default, and laziness implies indirections(pointers). Updating a lazy record field means first generating a thunk and pointing to that thunk from the record. When the thunk is evaluated, we get one more indirection: A new pointer pointing to the actual data². This means that we need two pointer dereferencing just to read a single Int from a record.

At this point garbage collector helps to eliminate one level of indirection, and updates the field to point to the data directly. But this waits until the next garbage collection.

GHC has some support for “unpacking” fields of ADTs and records. When a field is “unpacked”, it means that 1) the field is strict 2) the value is not allocated separately and pointed to by a pointer, it’s part of the data constructor/record³.

To illustrate how important unpacking is, I implemented two benchmarks. This is the data types I use in the benchmarks:

data GL a = GLNil | GLCons a (GL a)

data SGL a = SGLNil | SGLCons !a (SGL a)

data IntList = ILNil | ILCons {-# UNPACK #-} !Int IntList

The first type, GL, is the exactly the same as GHC’s standard list type. Second one is mostly the same, only difference is I have a strictness annotation(a BangPattern) before in the head(or car) part of the list. Third one is similar to second one, except I also unpack the car.

Note that if you look at the types, first two of these types are parametric on the list elements, while the third one is specialized to integers. This is essentially monomorphization, and some compilers can do that automatically in some cases(1, 2, if you know other compilers that do this, please write a comment), but in the presence of higher-order functions(and probably some other features), it’s in general not possible to monomorphise everything⁴. GHC has some limited support for this with the SPECIALIZE pragma, but it only works on functions and it doesn’t specialize data types(and maybe it can’t do this even in theory).

Now, I’m going to implement two functions on these data types. First function is for summing up all the elements:

glSum :: GL Int -> Int
glSum = glSumAcc 0

glSumAcc :: Int -> GL Int -> Int
glSumAcc !acc GLNil        = acc
glSumAcc !acc (GLCons h t) = glSumAcc (acc + h) t

I implement exactly the same function for other types too.

Second function is the length function:

glLength :: GL a -> Int
glLength = glLengthAcc 0

glLengthAcc :: Int -> GL a -> Int
glLengthAcc !acc GLNil        = acc
glLengthAcc !acc (GLCons _ l) = glLengthAcc (acc + 1) l

(Similarly for other two types..)

Now I’m going to benchmark these two function for all three variants, but let’s just speculate about what would be the expected results.

Clearly the third one should be faster for sum, because we don’t need to follow pointers for reading the integer. But should the second type(parametric but strict) be any faster? I’d say yes. The reason is because the field is strict, and so when we do pattern matching on Int to add integers, we don’t need to enter any thunks, we know that Int is already in WHNF. We should be able to just read the field.

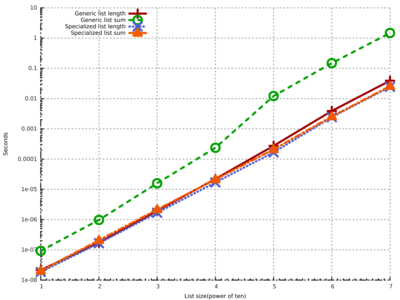
Here’s the result: (click on it to maximize)

As you can see I have an extra line in this plot: I added GHC’s standard lists and used standard sum function. It’s ridiculously slow, it’s almost two orders of magnitude slower on a list with length 10^7. Before moving on and interpreting rest of the lines let’s just talk a bit about why this is slower. We only need to look at the type of sum function:

sum :: (Foldable t, Num a) => t a -> a

This function is very, very general. There’s no way for this function to run fast, unless GHC is smart enough to generate a specialized version of this for [Int]. It turns out GHC is not smart enough, and in our case this is causing trouble. Note that we need two specializations here. First is to eliminate Foldable t part(we statically know that t is []), and second is to eliminate Num a part(we statically know that a is Int).

Now that we have this out of the way, let’s look at the other 3 lines. We can see that unboxed version is really faster(0.039 seconds other lists vs. 0.018 seconds unboxed list), which was expected. The interesting part is strict version is exactly the same as lazy version. Now, I don’t have a good explanation for this. The generated Core and STG for these two variants of sum are exactly the same. The Cmm or assembly code should be different. The problem is, I really can’t make any sense of generated Cmm code. I should study Cmm more for this.

But I have an idea: Pattern matching means entering the thunk to reveal the WHNF structure. Since our integers are boxed, we need to pattern match on them to read the primitive Int#s. This means entering the thunks, even if the field is strict.

In my benchmarks, I only used completely normalized lists. This means that in the lazy case we enter thunks, only to return immediately, because the Int is already in WHNF. There’s no difference in lazy and strict variants in pattern matching.

Only difference is when we update the field, in which case generated code should be different if the field is strict.

To validate the second part of this claim, I wrote another benchmark. In this benchmark I again create a list of length 10^7, but every cell has an integer calculated using a function. I then measure list generation and consumption(sum) times. The idea is that in the case of strict list, list generation should be slower, but consumption should be faster, and the opposite in the lazy list case. Indeed we can observe this in the output:

Performing major GC
Generating generic list
Took 0.737606563 seconds.
Performing major GC
Summing generic list
Took 0.490998969 seconds.
Performing major GC
Generating strict list
Took 0.870686580 seconds.
Performing major GC
Summing strict list
Took 0.035886157 seconds.

The program is here. We can see that summing strict list is 10x faster, but producing is slower, because instead of generating thunks we’re actually doing the work while producing cons cells.

(One thing to note here is that if the computation in thunks is not expensive enough, strict lists are faster in both production and consumption. I think the reason is because thunking overhead is bigger than actually doing the work in some cases)

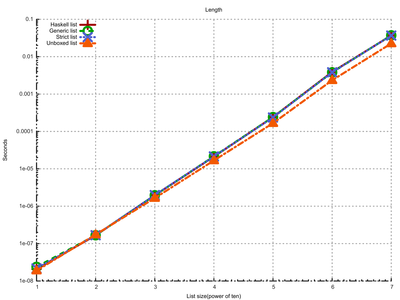
OK, I hope this explains the story with sum. The second part of the benchmark is even more interesting. It runs length. Here’s the plot:

We again have a line for standard Haskell list here. Good news is that even though standard length’s type is again very general, this time GHC was able to optimize:

length :: Foldable t => t a -> Int

Interesting part is that unboxed list is again faster! But why? We’re not using head fields, whether it’s a pointer or not should not matter, right?

Here I again have an idea: Even though we never use head parts, the garbage collector has to traverse all the data, and copy them from one generation to other.

(We also allocate more, but I’m not measuring that in the benchmarks)

To again back my claims, I have another set of benchmark programs that generate some GC stats. Here’s the output for “generic” case:

   800,051,568 bytes allocated in the heap
 1,138,797,344 bytes copied during GC
   310,234,360 bytes maximum residency (12 sample(s))
    68,472,584 bytes maximum slop
           705 MB total memory in use (0 MB lost due to fragmentation)

                                   Tot time (elapsed)  Avg pause  Max pause
Gen  0      1520 colls,     0 par    0.207s   0.215s     0.0001s    0.0009s
Gen  1        12 colls,     0 par    0.348s   0.528s     0.0440s    0.1931s

INIT    time    0.000s  (  0.000s elapsed)
MUT     time    0.126s  (  0.082s elapsed)
GC      time    0.555s  (  0.743s elapsed)
EXIT    time    0.004s  (  0.050s elapsed)
Total   time    0.685s  (  0.875s elapsed)

%GC     time      81.0%  (84.9% elapsed)

Alloc rate    6,349,615,619 bytes per MUT second

Productivity  19.0% of total user, 14.9% of total elapsed

“Generic strict” case:

   800,051,568 bytes allocated in the heap
 1,138,797,344 bytes copied during GC
   310,234,360 bytes maximum residency (12 sample(s))
    68,472,584 bytes maximum slop
           705 MB total memory in use (0 MB lost due to fragmentation)

                                   Tot time (elapsed)  Avg pause  Max pause
Gen  0      1520 colls,     0 par    0.211s   0.213s     0.0001s    0.0008s
Gen  1        12 colls,     0 par    0.367s   0.531s     0.0442s    0.1990s

INIT    time    0.000s  (  0.000s elapsed)
MUT     time    0.114s  (  0.080s elapsed)
GC      time    0.578s  (  0.744s elapsed)
EXIT    time    0.003s  (  0.045s elapsed)
Total   time    0.698s  (  0.869s elapsed)

%GC     time      82.8%  (85.6% elapsed)

Alloc rate    7,017,996,210 bytes per MUT second

Productivity  17.2% of total user, 13.8% of total elapsed

“Unboxed” case:

   560,051,552 bytes allocated in the heap
   486,232,928 bytes copied during GC
   123,589,752 bytes maximum residency (9 sample(s))
     3,815,304 bytes maximum slop
           244 MB total memory in use (0 MB lost due to fragmentation)

                                   Tot time (elapsed)  Avg pause  Max pause
Gen  0      1062 colls,     0 par    0.117s   0.123s     0.0001s    0.0018s
Gen  1         9 colls,     0 par    0.116s   0.179s     0.0199s    0.0771s

INIT    time    0.000s  (  0.001s elapsed)
MUT     time    0.070s  (  0.054s elapsed)
GC      time    0.233s  (  0.302s elapsed)
EXIT    time    0.002s  (  0.019s elapsed)
Total   time    0.306s  (  0.376s elapsed)

%GC     time      76.1%  (80.4% elapsed)

Alloc rate    8,000,736,457 bytes per MUT second

Productivity  23.9% of total user, 19.4% of total elapsed

Interesting parts are productivity rates and total bytes allocated. We can see that unboxed version is a lot better in both.

The reason why productivities are too bad in all cases is, I think, that because this is purely an allocation benchmark, all we do is to allocate and then we do one pass on the whole thing. In this type of programs it makes sense to increase the initial heap a little bit to increase the productivity. For example, if I use -H1G productivity increases to 64% in generic list case and to 97% in unboxed list case.

So what’s the lesson here?

The data layout matters a lot. Even if the data is not used in some hot code path, GC needs to traverse all the live data and in the case of GHC Haskell it needs to copy them in each GC cycle. Also, lazy-by-default is bad for performance.

An improvement

I recently finished implementing hard parts of a project. I don’t want to give too much detail here for now but let’s just say we’re improving the unboxing story in GHC. With our new patch, you will be able to {-# UNPACK #-} some of the types that you can’t right now. When/if the patch lands I’m going to announce it here.

With -XStrictData, -XStrict and flags like -funbox-strict-fields(search for it here) we’ll have a lot better story about data layout than we have today. But there are still some missing pieces. Our patch will hopefully implement one more missing piece and we’ll have even better data layout story.

I think the next step then will be better calling conventions for strict functions and some other tweaks in the runtime system for better strict code support overall. Then maybe we can officially declare Haskell as a language with lazy and strict evaluation ;-) .